红黑树相关代码

红黑树

最近面试老是被问到红黑树，堪称灵魂拷问：

面试官：Java的HashMap在JDK1.8之后用的是红黑树，那你知道红黑树是什么吗？

我：是一个自平衡的二叉排序树吧。

面试官：能不能跟我细细说一下红黑树呢？

我：底层源代码没有看过。

面试官：那你走吧。

太真实了，那今天就看看红黑树的底层是怎么实现的吧。

什么是红黑树？

红黑树是一种含有红黑结点并能自平衡的二叉查找树。

什么是二叉平衡树？

左右子树的高度相差不超过 1 的树为平衡二叉树。

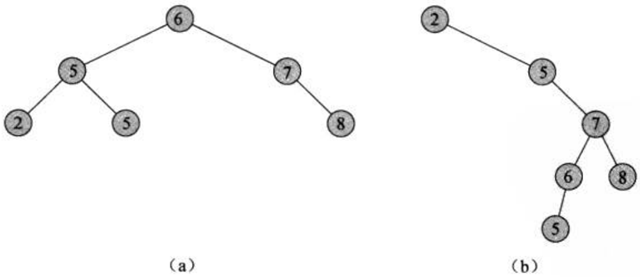
图中(a)是二叉平衡树（b）不是二叉平衡树

什么是二叉查找树？

二叉查找树（BST：Binary Search Tree）是一种特殊的二叉树，它改善了二叉树节点查找的效率。二叉查找树有以下性质：

对于任意一个节点 n，

• 其左子树（left subtree）下的每个后代节点（descendant node）的值都小于节点 n 的值；
• 其右子树（right subtree）下的每个后代节点的值都大于节点 n 的值。

上面的（a）和（b）都是二叉查找树

红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质：

• 性质1：每个节点要么是黑色，要么是红色。
• 性质2：根节点是黑色。
• 性质3：每个叶子节点（NIL）是黑色。
• 性质4：每个红色结点的两个子结点一定都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
• 性质5：从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点

从性质5又可以推出：

• 性质5.1：如果一个结点存在黑子结点，那么该结点肯定有两个子结点

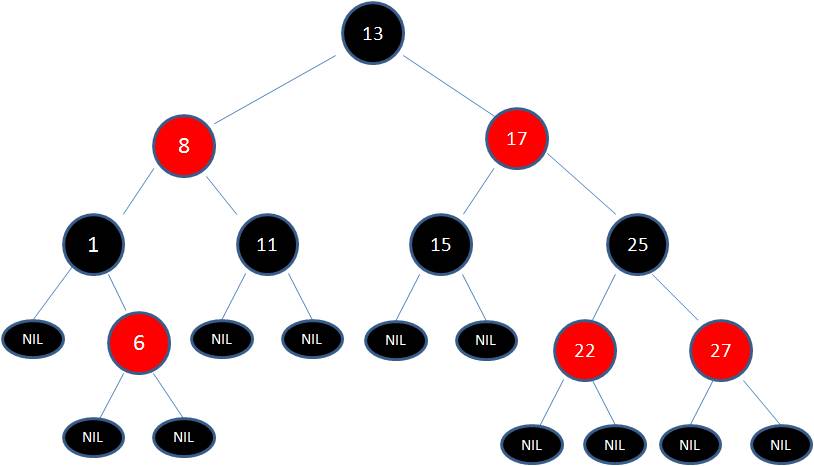
这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

怎么得出这个结论的呢？

性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

红黑树有什么用呢，为什么要出现这个树结构呢？

相比于BST，因为红黑树可以能确保树的最长路径不大于两倍的最短路径的长度，所以可以看出它的查找效果是有最低保证的。在最坏的情况下也可以保证O(logN)的，这是要好于二叉查找树的。因为二叉查找树最坏情况可以让查找达到O(N)。

比如这样：

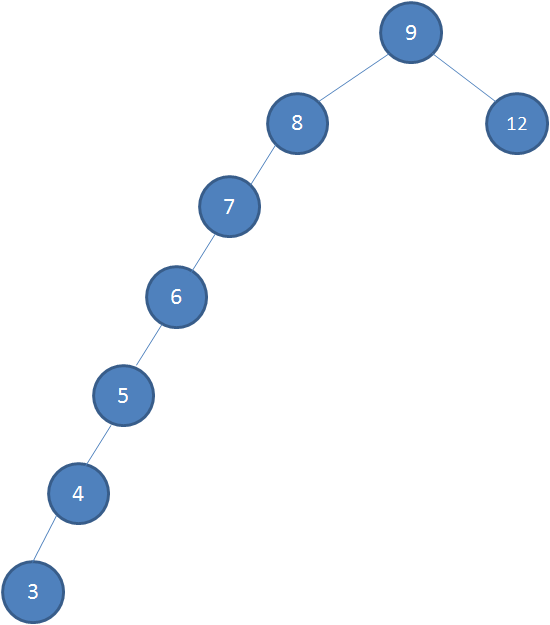
与二叉平衡树相比：

红黑树的算法时间复杂度和AVL相同，但统计性能比AVL树更高，所以在插入和删除中所做的后期维护操作肯定会比红黑树要耗时好多，但是他们的查找效率都是O(logN)，所以红黑树应用还是高于AVL树的. 实际上插入 AVL 树和红黑树的速度取决于你所插入的数据.如果你的数据分布较好,则比较宜于采用 AVL树(例如随机产生系列数),但是如果你想处理比较杂乱的情况,则红黑树是比较快的。

红黑树怎么保证自平衡的？

约定一下红黑树中节点的名称：

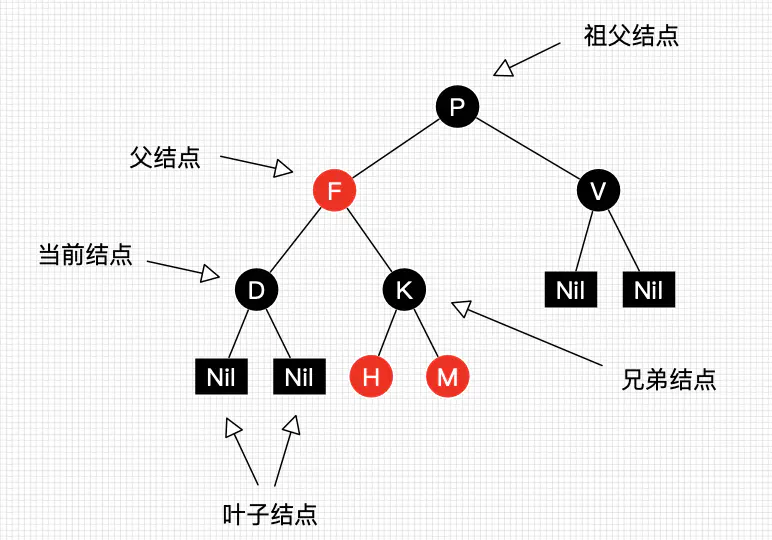
红黑树能自平衡，它靠的是什么？三种操作：左旋、右旋和变色。

左旋：以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。如图3。

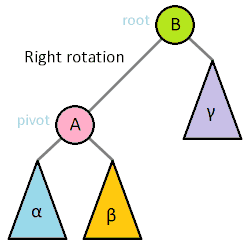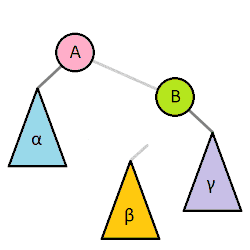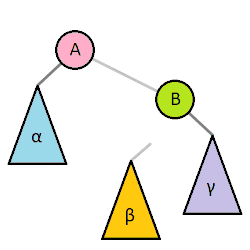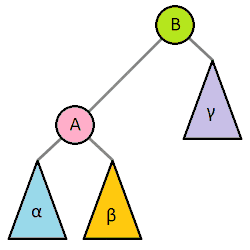
右旋：以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。如图4。

变色：结点的颜色由红变黑或由黑变红。

左旋

右旋

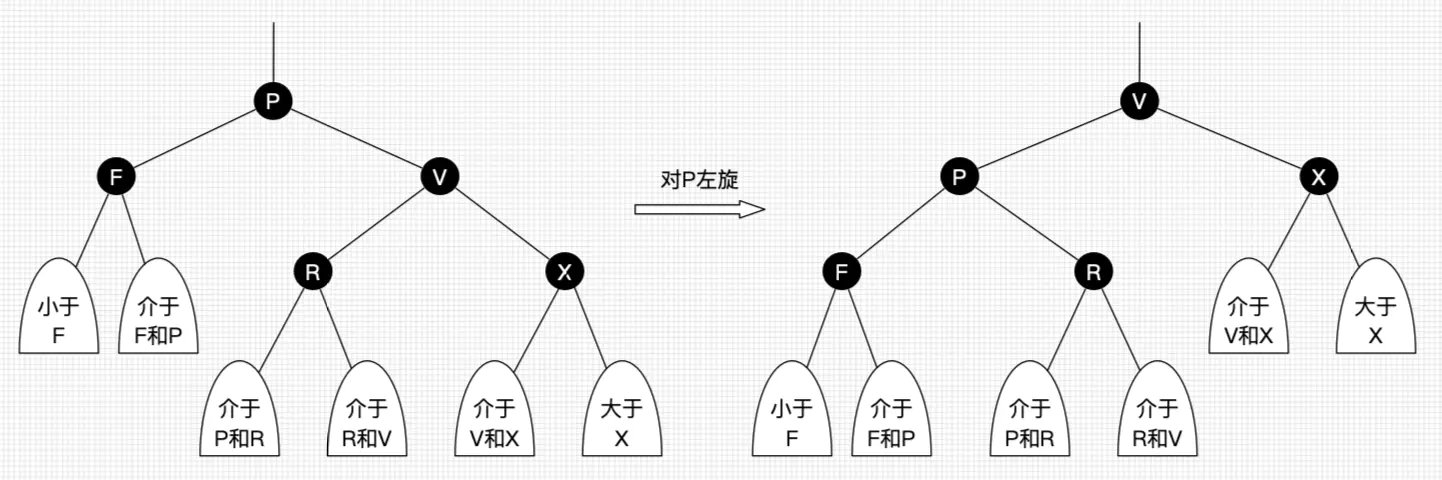
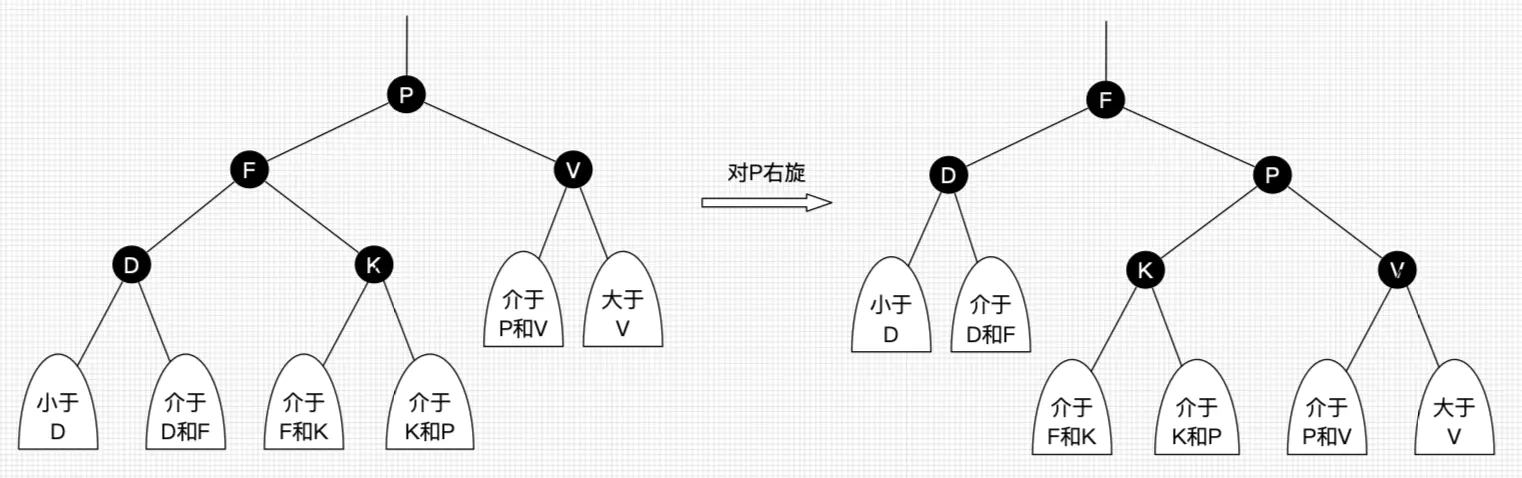
我们先忽略颜色，可以看到旋转操作不会影响旋转结点的父结点，父结点以上的结构还是保持不变的。
左旋只影响旋转结点和其右子树的结构，把右子树的结点往左子树挪了。
右旋只影响旋转结点和其左子树的结构，把左子树的结点往右子树挪了。

红黑树如何进行插入

插入操作包括两部分工作：首先是先找到插入的位置，然后就是把节点插入之后看树结构有没有平衡，如果没平衡的话那么就去利用上述红黑树的特征进行自平衡。

插入的流程：

1. 从根结点开始查找；
2. 若根结点为空，那么插入结点作为根结点，结束。
3. 若根结点不为空，那么把根结点作为当前结点；
4. 若当前结点为null，返回当前结点的父结点，结束。
5. 若当前结点key等于查找key，那么该key所在结点就是插入结点，更新结点的值，结束。
6. 若当前结点key大于查找key，把当前结点的左子结点设置为当前结点，重复步骤4；
7. 若当前结点key小于查找key，把当前结点的右子结点设置为当前结点，重复步骤4；

找到插入节点之后，我们对节点进行插入，那么插入的时候节点颜色应该是上面颜色呢？答案是红色，原因是红色在父结点（如果存在）为黑色结点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。但如果插入结点是黑色，那么插入位置所在的子树黑色结点总是多1，必须做自平衡。

做一个约定：

将要插入的节点标为N，N的父节点标为P，N的祖父节点标为G，N的叔父节点标为U。在图中展示的任何颜色要么是由它所处情形这些所作的假定，要么是假定所暗含（imply）的。

插入的几种方式：

• 情形1:新节点N位于树的根上，没有父节点。
• 情形2:新节点的父节点P是黑色（新节点是红色的）。
• 情形3:如果父节点P和叔父节点U二者都是红色
• 情形4:父节点P是红色而叔父节点U是黑色或缺少，并且新节点N是其父节点P的右子节点而父节点P又是其父节点的左子节点。
• 情形5:父节点P是红色而叔父节点U是黑色或缺少，新节点N是其父节点的左子节点，而父节点P又是其父节点G的左子节点。

我们就一个一个来分析这几种情况：

1、新节点N位于树的根上，没有父节点。

这时候我们只需要把节点加入进去，然后把节点的颜色换成黑色，因为根据规则二，根节点必须为黑色。

代码：

void insert_case1(node *n){
    if(n->parent == NULL)
        n->color = BLACK;
    else
        insert_case2 (n);
}

2、新节点的父节点P是黑色

在这种情形下，树仍是有效的。性质5也未受到威胁，尽管新节点N有两个黑色叶子子节点；但由于新节点N是红色，通过它的每个子节点的路径就都有同通过它所取代的黑色的叶子的路径同样数目的黑色节点，所以依然满足这个性质。

void insert_case2(node *n){
    if(n->parent->color == BLACK)
        return; /* 树仍旧有效*/
    else
        insert_case3 (n);
}

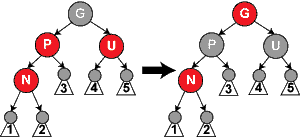
3、如果父节点P和叔父节点U二者都是红色

此时新插入节点N做为P的左子节点或右子节点都属于情形3,下图仅显示N做为P左子的情形，则我们可以将它们两个重绘为黑色并重绘祖父节点G为红色（用来保持性质5）。现在我们的新节点N有了一个黑色的父节点P。因为通过父节点P或叔父节点U的任何路径都必定通过祖父节点G，在这些路径上的黑节点数目没有改变。但是，红色的祖父节点G可能是根节点，这就违反了性质2，也有可能祖父节点G的父节点是红色的，这就违反了性质4。为了解决这个问题，我们在祖父节点G上递归地进行情形1的整个过程。（把G当成是新加入的节点进行各种情形的检查）

void insert_case3(node *n){
    if(uncle(n) != NULL && uncle (n)->color == RED) {
        n->parent->color = BLACK;
        uncle (n)->color = BLACK;
        grandparent (n)->color = RED;
        insert_case1(grandparent(n));
    }
    else
        insert_case4 (n);
}

4、父节点P是红色而叔父节点U是黑色或缺少，并且新节点N是其父节点P的右子节点而父节点P又是其父节点的左子节点

因为有点绕，先看看图，再进行分析：

旋转示意图

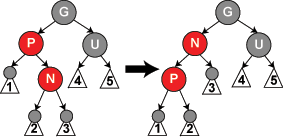
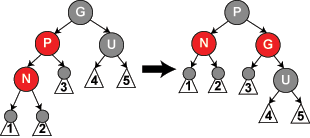
在这种情形下，我们进行一次左旋转调换新节点和其父节点的角色;接着，我们按情形5处理以前的父节点P以解决仍然失效的性质4。注意这个改变会导致某些路径通过它们以前不通过的新节点N（比如图中1号叶子节点）或不通过节点P（比如图中3号叶子节点），但由于这两个节点都是红色的，所以性质5仍有效。

void insert_case4(node *n){
     if(n == n->parent->right && n->parent == grandparent(n)->left) {
         rotate_left(n);
         n = n->left;
     } else if(n == n->parent->left && n->parent == grandparent(n)->right) {
         rotate_right(n);
         n = n->right;
     }
     insert_case5 (n);
 }

5、父节点P是红色而叔父节点U是黑色或缺少，新节点N是其父节点的左子节点，而父节点P又是其父节点G的左子节点

因为有点绕，先看看图，再进行分析：

在这种情形下，我们进行针对祖父节点G的一次右旋转；在旋转产生的树中，以前的父节点P现在是新节点N和以前的祖父节点G的父节点。我们知道以前的祖父节点G是黑色，否则父节点P就不可能是红色（如果P和G都是红色就违反了性质4，所以G必须是黑色）。我们切换以前的父节点P和祖父节点G的颜色，结果的树满足性质4。性质5也仍然保持满足，因为通过这三个节点中任何一个的所有路径以前都通过祖父节点G，现在它们都通过以前的父节点P。在各自的情形下，这都是三个节点中唯一的黑色节点。

void insert_case5(node *n){
    n->parent->color = BLACK;
    grandparent (n)->color = RED;
    if(n == n->parent->left && n->parent == grandparent(n)->left) {
        rotate_right(n->parent);
    } else {
        /* Here, n == n->parent->right && n->parent == grandparent (n)->right */
        rotate_left(n->parent);
    }
}