排序代码复习

复习一下各个排序的代码，加深理解。

首先看一下各个排序算法的时间复杂度：

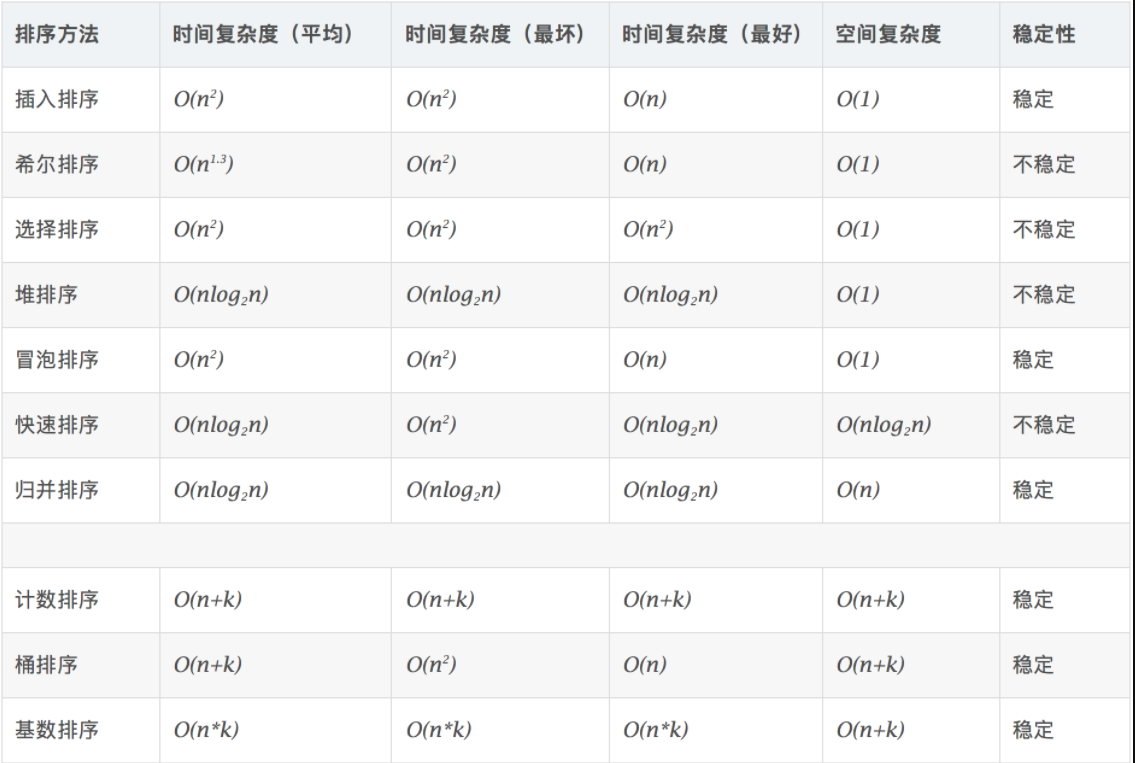
冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

public static void bubbleSort(int[] nums) {
    for (int i = 0; i < nums.length - 1; i++) {
        for (int j = 0; j < nums.length - 1 -i; j++) {
            if (nums[j] > nums[j + 1]) {
                int temp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = temp;
            }
        }
    }
}

复杂度:

平均：$O(n^2)$ 最好 :$O(n)$ 最坏:$O(n^2)$ 稳定性：稳定

选择排序（Selection Sort）

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

public static void selectionSort(int[] nums) {
    for (int i = 0; i < nums.length - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] < nums[minIndex]) {
                minIndex = j;
            }
        }
        int temp= nums[minIndex];
        nums[minIndex]=nums[i];
        nums[i]=temp;
    }
}

平均：$O(n^2)$ 最好 :$O(n^2)$ 最坏:$O(n^2)$ 稳定性：不稳定

插入排序（Insertion Sort）

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

public static void insertionSort(int[] nums) {
    int preIndex, now;
    for (int i = 1; i < nums.length; i++) {
        preIndex = i - 1;
        now = nums[i];
        while (preIndex >= 0 && nums[preIndex] > now) {
            nums[preIndex + 1] = nums[preIndex];
            preIndex--;
        }
        nums[preIndex+1] = now;
    }

}

平均：$O(n^2)$ 最好 :$O(n)$ 最坏:$O(n^2)$ 稳定性：稳定

希尔排序（Shell Sort）

1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

算法描述：

• 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
• 按增量序列个数k，对序列进行k 趟排序；
• 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

public static void shellSort(int[] nums) {
    for (int step = nums.length / 2; step > 0; step /= 2) {
        //先分组，组数每次变为原来的1/2
        for (int i = step; i < nums.length; i++) {
            //从增量那组进行插入排序，直到完毕
            int j = i;
            int temp = nums[j];
            while (j-step>=0&&nums[j-step]>temp){
                nums[j]= nums[j-step];
                j=j-step;
            }
            nums[j]=temp;
        }
    }
}

快速排序（Quick Sort）

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

public static void quickSort(int[] nums) {
    quickSortSub(nums, 0, nums.length - 1);
}

public static void quickSortSub(int[] nums, int start, int end) {
    if (start > end) {
        return;
    }
    int i = start;
    int j = end;
    int benchmark = nums[i];
    int temp;
    while (i < j) {
        while (i < j && benchmark <= nums[j]) {
            j--;
        }
        while (i < j && benchmark >= nums[i]) {
            i++;
        }
        temp = nums[j];
        nums[j] = nums[i];
        nums[i] = temp;
    }
    nums[start]= nums[i];
    nums[i]=benchmark;
    quickSortSub(nums,start,i-1);
    quickSortSub(nums,i+1,end);
}

平均：$O(nlog_2n)$ 最好 :$O(nlog_2n)$ 最坏:$O(n^2)$ 稳定性：不稳定

归并排序（Merge Sort）

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

public static void mergeSort(int[] nums) {
    int[] temp = new int[nums.length];
    sort(nums, 0, nums.length - 1, temp);
}

public static void sort(int[] nums, int left, int right, int[] temp) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        sort(nums, 0, mid, temp);
        sort(nums, mid + 1, right, temp);
        merge(nums, left, mid, right, temp);
    }
}

public static void merge(int[] nums, int left, int mid, int right, int[] temp) {
    //左序列指针
    int i = left;
    //右序列指针
    int j = mid + 1;
    //temp指针
    int t = 0;
    while (i <= mid && j <= right) {
        if (nums[i] <= nums[j]) {
            temp[t++] = nums[i++];
        } else {
            temp[t++] = nums[j++];
        }
    }
    while (i <= mid) {
        temp[t++] = nums[i++];
    }
    while (j <= right) {
        temp[t++] = nums[j++];
    }
    t=0;
    while(left <= right){
        nums[left++] = temp[t++];
    }
}

平均：$O(nlog_2n)$ 最好 :$O(nlog_2n)$ 最坏:$O(nlog_2n)$ 稳定性：稳定

堆排序（Heap Sort）

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

public static void heapSort(int[] nums) {
    for (int i = nums.length / 2 - 1; i >= 0; i--) {
        //从第一个非叶子结点从下至上，从右至左调整结构
        adjustHeap(nums, i, nums.length);
    }
    for (int i = nums.length - 1; i >= 0; i--) {
        //将堆顶元素与末尾元素进行交换
        swap(nums, 0, i);
        //重新调整
        adjustHeap(nums, 0, i);
    }
}

public static void adjustHeap(int[] nums, int i, int len) {
    int temp = nums[i];
    //从i结点的左子结点开始，也就是2i+1处开始
    for (int k = i * 2 + 1; k < len; k = k * 2 + 1) {
        //如果左子结点小于右子结点，k指向右子结点
        if (k + 1 < len && nums[k] < nums[k + 1]) {
            k++;
        }
        //如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
        if (nums[k] > temp) {
            nums[i] = nums[k];
            i = k;
        } else {
            break;
        }
    }
    nums[i]=temp;
}

public static void swap(int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

平均：$O(nlog_2n)$ 最好 :$O(nlog_2n)$ 最坏:$O(nlog_2n)$ 稳定性：不稳定

本文就是笔者关于排序算法的一次记录，以便加深理解，如果需要详细了解具体的排序算法，请参考其他博主对这些排序算法的讲解，如果有好的建议，希望大家指出！